학습 주제
- 확률과 확률변수
- 확률분포
- 기술통계
- 가설검정
주요 학습내용
- 확률
- 통계학 : 여러 사건(event)들을 수학적으로 모델링하고, 이를 분석하는 것이 통계학의 본질
- 사건은 근본적으로 발생하기 전에는 알 수 없으므로 불확실성을 내포하고 있다. 불확실성을 표현할 수 있는게
확률 - 예시) 동전 두번 던지기
Experiment : 동전을 던지는 행위
Sample : experiment의 결과(동전의 앞/뒤)
Sample space : experiment 로 인해 발생하는 모든 Sample의 집합
Event : sample space의 부분 집합으로, 어떤 조건을 만족하는 특정한 표본점들의 집합
이 때, sample space S는 다음과 같다.
S = {(앞, 앞), (앞, 뒤), (뒤, 앞), (뒤, 뒤)} - 확률 : 실험을 실시했을 때, 나올 수 있는 모든 경우의 수(sample space)내 에서 특정 사건이 발생하는 비율

- 동전 한번 던지기 예시
sample space S ={앞, 뒤}
event A = 앞 이라고 할때
동전 앞면이 나올 확률
- 확률의 성질
- 사건 A가 발생할 확률은 [0, 1] 사이의 값을 가진다.
- Sample space 내 모든 사건의 확률의 합은 1이다.

Ω = sample space, ∈ = 소속되어있다,
- 변수
- 변수(Variable) : 특정 조건에 따라 변하는 값
-> 확률 변수는 '확률'에 따라 변하는 값 - 독립 변수 (x, feature) : 다른 변수에 영향을 받지 않는 오히려 종속 변수에 영향을 주는 변수
- 종속 변수 (y, label) : 독립 변수의 영향을 받아서 변화하는 변수
- 연구자의 목표는 독립변수를 조정할 때 종속 변수가 어떻게 변화하는지를 알아내는 것이다.
"독립 변수가 원인, 종속 변수가 결과" 라는 가정이 필요, 두 변수간의 관계를 알아내는 것이 중요하다.
- 변수(Variable) : 특정 조건에 따라 변하는 값
- 확률 변수
- 확률 변수(Random Variable) : 무작위 실험 시 특정 확률로 발생하는 각각의 결과를 수치화한 변수
- 이산 확률 변수 (Discrete random variable) : 확률 변수 X가 이산값(정수) 값을 택하는 변수
- 연속 확률 변수 (Continuous random variable) : 확률 변수 X가 어떤 구간의 모든 실수값 택하는 변수
- ex) 동전 두번 던져 앞이 나오는 확률 변수 일 때 X가 가질 수 있는 값 = {0, 1, 2} 확률 분포
=> 0 (0.25), 1(0.5), 2(0.25) - 확률 함수 : 확률 번수 x 를 확률값에 대응시키는(연결시키는) 함수 P(x)
- 확률 변수와 확률 함수를 이용해 sample space내 사건의 확률 얻을 수 있다.
sample space -> [확률 변수 X] -> 실수 공간 -> [확률 함수 f(x)] -> 확률
ex) 주사위를 두번 던져서 나온 합이 5이상 7이하인 확률?
=> X sample space ={2,3,...,12}
P(5<=X<=7) = P(X=5) + P(X=6) + P(X=7) = 4/36 + 5/36 + 6/36 = 5/12
정규분포를 따르는 확률 변수 X가 (μ-2σ) 와 (μ+2σ) 사이의 값을 가질 확률

정규분포 성질 중 하나인 68-95-99.7 규칙을 따른다.
- 확률질량함수
- 확률질량함수 P(X = x) : 이산확률변수 X가 취할 수 있는 값 x0, x1, .. 의 각각에 대해 확률값 P(X=x0), P(X=x1),.. 를 대응시켜주는 확률 함수
- 확률질량함수의 성질
- 비음수성 : 확률질량함수는 모든 x에 대해 비음수이다 P(X=x) >= 0
- 정규화 : 모든 가능한 x 값에 대해 확률질량함수의 합은 1이다, 확률변수 X 가 어떤 값은 반드시 가진다.

- 특정값의 확률 : P(X = x)는 확률변수 X가 특정 값 x를 취할 확률을 나타낸다.
- 누적확률 : 두 값 a와 b에 대해, P(a <= X <= b)는 a 와 b 사이의 모든 값들에 대한 PMF의 합으로 계산된다.

- 기대값과 분산 : 확률 질량함수를 사용하여 확률변수의 기대값(평균)가 분산을 계산 할 수 있다.

- 확률밀도함수
- 확률밀도함수(Probability Density Function, pdf) : 연속 확률변수의 확률 분포를 설명하는 함수, 특정 구간 내의
값을 가질 확률을 나타내는데 사용된다. - 성질
- 비음수성 : 모든 x 에 대해 비음수이다. f(x) >= 0
- 정규화 : 확률밀도함수의 전체 정의역에 대한 적분은 1이다. => 정의역 안의 어떤값은 반드시 가진다.

- 확률의 계산 : 연속 확률변수 X가 a와 b 사이의 값들을 가질확률은 a와 b사이의 확률 밀도함수를 적분하여
구할 수 있다.
- 누적 분포 함수 (CDF) : 누적분포 함수 F(x)는 확률밀도함수 f(x)의 적분으로 정의되며, 확률변수 X가 특정 값
x 보다 작거나 같을 확률을 나타낸다.
- 기대값과 분산 : 확률밀도함수를 이용하여 확률변수의 기대값(평균)과 분산을 계산할 수 있다.

- 함수의 특성
- 확률밀도함수는 확률변수의 값에 대한 밀도를 나타낸다. PDF의 특정 지점에서의 값 자체가
확률이 아닌, 해당 지점 근방의 작은 구간에서 확률을 구하기 위한 밀도로 해석해야한다.
- 실제 확률은 PDF 위의 구간을 적분하여 구한다. - 그래프의 특성
- PDF 그래프 아래의 총 면적은 1과 같다, 즉 모든 가능한 결과의 확률이 1(100%)이다.
- 그래프의 특정 부분 아래의 면적은 해당 구간의 확률을 나타낸다. PDF 특정 구간에서 적분하여 구함
- 확률밀도함수(Probability Density Function, pdf) : 연속 확률변수의 확률 분포를 설명하는 함수, 특정 구간 내의
- 모집단, 모수, 표본
- 모집단 : 통계학에서 관심의 대상이 되는 모든 개체 값의 집합
- 모수(Population parameter, Parameter) : 모집단의 특성을 나타내는 통계적인 특성치
- 모집단이 정규분포를 따르면 모집단의 분포 특성을 나타내는 모수는 μ(평균)과 σ2(표준편차) - 모수는 모집단을 모두 조사(전수검사) 해야 얻을 수 있는 값이지만, 전수검사가 어렵기 때문에 "통계적 추론"한다.
- 통계적 추론 : 모집단에서 추출한 표본들의 특성을 분석하여 ,모수에 대해 추론하는 과정 - 표본(sample) : 전체 모집단에 대해서 샘플링(sampling)을 통해 뽑히는 값으로, 모집단의 부분 집합을 의미한다.
- 전반적 프로세스
- 모집단이 갖는 분포를 가정한다.(정규분포, 포아송분포,..)
- sample들을 추출한다
- 뽑힌 sample들을 통해 얻어진 통계량(평균, 분산,..)이 지닌 성질을 이용해 모수를 추정한다.
- 모집단의 모수를 잘 추정하기 위해선 표본을 잘 추출해야한다.
- 모집단에서 sample이 뽑힐 가능성을 모두 '동일'하게 부여하고, 객관적으로 무작위 추출해야한다.
- sample 들을 서로 독립적이며 동일한 분포 (i.i.d)를 따라야 한다
독립적 : sample들이 추출될 때 서로 영향을 미치지 않는다.
동일한 분포 : sample들이 동일한 모집단으로부터 추출된다.
- sample들의 통계량은 추출할 때 마다 달라지지만, 여러번의 추출을 통해 얻어진 여러 통계량 값의 발생 분포를
그리면 통계량을 확률 변수로 하는 확률 변수를 얻을 수 있다.
=> 통계량의 확률 함수와 확률 분포를 이용하여 모수를 추정할 수 있다.
- 기댓값 & 분산
- 기댓값(Expected value) : 어떤 확률적 사건이 평균적으로 가질 수 있는 값(=평균값, E(x), μ)
- 이산확률변수의 기댓값

- 연속확률변수의 기댓값

- 기댓값의 성질
- E(X + Y) = E(X) + E(Y)
- 임의의 실수 a, b, c에 대해서
E(aX+b) = aE(X)+b - E(aX2 + bX + c) = aE(X2) + bE(X) + c
- E(aX + bY) = aE(X) + bE(Y)
- 서로 독립인 두 확률변수 X, Y에 대해서
E(XY) = E(X)E(Y)
- 분산 : 분포가 평균값으로부터 얼마나 산포되어있는지 (Var(X), σ2)

- 이산확률변수의 분산

- 연속확률변수의 분산

- 표준편차
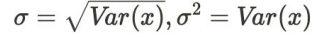
- 분산의 성질
- 서로 독립인 두 확률변수 X, Y에 대해서
Var(X + Y) = Var(X) + Var(Y) - 임의의 실수 a, b, c에 대해서
Var(aX+b) = a2Var(X)
Var(aX+bY) = a2Var(X)+ b2Var(Y)
- 서로 독립인 두 확률변수 X, Y에 대해서
- 결합확률분포
- 두 개의 확률 변수 X, Y에 대해 P(X=x, Y=y)=f(x,y)를 만족하는 f(x,y)를 확률변수 X, Y의 결합확률분포혹은 결합확률{질량/밀도}함수(Joint pmf/pdf) 라고 합니다
- 이산확률변수 X, Y의 결합확률은


- 연속확률변수 X, Y의 결합확률은


- 확률변수 X와 Y가 서로 독립이면

- 공분산
- 두 개의 확률변수 X와 Y에 대해 X 가 변할 때 Y가 변하는 정도를 나타내는 값이다.
X와 Y가 같이 변하는 정도를 나타내는 값
편차의 곲의 기댓값 E[ 편차 ] - 이산확률변수 공분산

- 연속확률변수 공분산
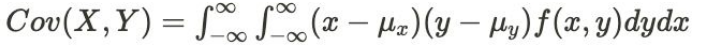
- 두 개의 확률변수 X와 Y에 대해 X 가 변할 때 Y가 변하는 정도를 나타내는 값이다.
- 베르누이 분포 (Bernoulli distribution)
- 베르누이시행 : 어떤 시행 결과가 1(성공) or 0(실패)인 실험
- p = 확률변수 X=1일 확률, q = 1-p 인 경우 확률변수 X는 베르누이 분포를 따른다.
- pmf

- 기댓값 E(X) = 1Xp + 0X(1-p) = p
E[x^2] = 1^2Xp + 0^2X(1-p) = p
분산 Var(X) = E[X^2] - E[X]^2 = p-p^2 = p(1-p)
- 이항 분포 (Binomial distribution)
- 베르누이 시행을 n번 반복했을 때 성공 횟수를 값으로 갖는 확률 변수 X에 대한 X
- 베르누이 시행의 결과가 성공할 확률 : p
- 실패할 확률 (1-p) , 이 시행을 n 번 반복했을 때 나타나는 확률분포
- 기댓값과 분산

- 포아송 분포 (Poisson distribution)
- 모수 람다는 '단위시간 / 단위공간에서의' 평균 발생횟수
- 단위시간 / 단위공간에서 어떤 사건이 발생하는 횟수를 확률변수 X라 할때의 X
- 포아송 분포의 전제조건
- 독립성 : 단위 시간 / 공간에서 발생한 결과는 중복되지 않은 다른 시간 /공간에서 발생한 결과와 독립
- 일정성 : 단위시간 / 공간에서 발생한 확률 / 횟수는 그 시간 / 공간의 크기에 비례한다.
=> 단위시간 / 공간에서 발생한 평균발생횟수는 일정하다 - 비집락성 : 매우 짧은(거의 같은) 시간 / 공간에서 두 개 이상의 결과가 동시에 발생한 확률은 0이다.
- pmf


- 균등분포 (Uniform distribution)
- 모든 확률변수값에 대해 균일한 확률을 갖는 확률 분포
- 구간 [a, b] 내 모든 구간에서 일정한 크기의 확률을 가지는 확률변수 X의 pdf


- 모든 확률의 합은 1이므로, 구간 [a,b]사이의 모든 확률의 합은 1이다.
- 정규분포 (Normal distribution)
- 가장 일반적으로 발견되는 양방향 대칭의 종 모양(Bell curve)으로 생긴 분포, 수집된 자료의 분포를 근사할 때
대부분 정규분포를 사용한다. (중심 극한정리에 의해 독립적인 확률 변수들의 평균이 정규분포에 가까워진다.)
- 가장 일반적으로 발견되는 양방향 대칭의 종 모양(Bell curve)으로 생긴 분포, 수집된 자료의 분포를 근사할 때
- 이항분포의 정규분포 근사
- 이항분포의 pmf 에서 n-> 무한대 극한으로 보낼 경우에 X의 확률(히스토그램)을 그리면 N(np, np(1-p))의 분포에
가까워 지는 것을 알 수 있다. (드무아브르-라플라스 정리)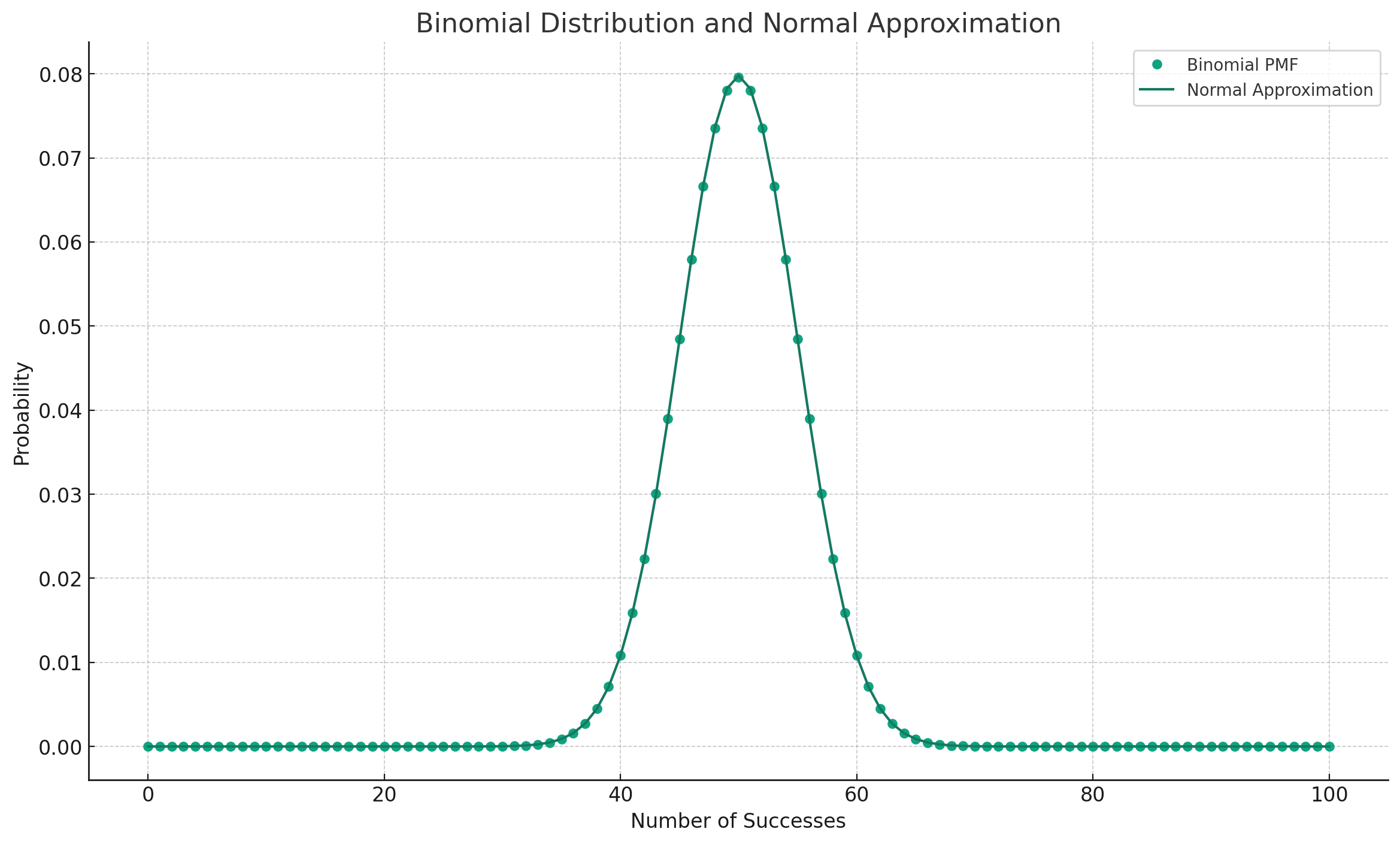
- 이항분포의 pmf 에서 n-> 무한대 극한으로 보낼 경우에 X의 확률(히스토그램)을 그리면 N(np, np(1-p))의 분포에
- 표준 정규 분포(Standard normal distribution)
- 서로다른 parameter를 가진 집단들을 비교하기 위해 정규분포를 표준화한 분포
=> 평균이 0, 표준편차가 1인 분포로 표준화 된다.
- 서로다른 parameter를 가진 집단들을 비교하기 위해 정규분포를 표준화한 분포
- 중심극한정리 (Central Limit Theorem)
- 서로 다른 여러 분포들의 표본 평균은 n이 커질수록 정규분포에 근사한다.
- 표본들의 합에 대해서도 중심극한 정리가 적요된다.
- n개의 표본이 특정 분포를 따르는 것이 아니고, n개 표본의 평균값이 n → ∞이면 (보통은 n>30)
정규분포를 따르는 것입니다.
공부하며 어려웠던 점
- 이론을 막 배웠는데 잘 써먹을 수 있을지 미지수다 데이터 가지고 연습해봐야겠다.
반응형
'데이터분석' 카테고리의 다른 글
| 33-(1) Matplotlib Visualization - 기본문법 (1) | 2024.01.14 |
|---|---|
| 32-(2). 정량적 데이터 분석 (1) | 2024.01.14 |
| 31. 정규화, 데이터 스케일링 (2) | 2024.01.10 |
| 30. 문자열 제어 및 DataFrame 재구성 (0) | 2024.01.09 |
| 29 Jupyter- DataFrame 심화 (0) | 2024.01.08 |