주요 학습 내용
- 정량적 데이터 분석
- 숫자로 표현되는 수치 데이터를 이용하여 주어진 데이터를 분석하는 과정이다.
- 평균, 중앙값, 최빈값을 통해 데이터가 어느 값을 중심으로 뭉쳐있는지를 확인합니다.
- 분산, 표준편차, 분위수, Q1(25분위수), Q3(75분위수)를 통해 데이터가 어떤 형태로 퍼져있는지를 확인합니다.
- describe()
- 전반적인 주요 통계를 확인할 수 있다. 기본 값으로 수치형(Numerical)칼럼에 대한 통계표를 보여준다. - df.count()
- 칼럼당 데이터의 개수 - df.mean()
- 칼럼당 데이터의 평균
- 기술통계 함수들에서 skipna=False로 설정시 NaN값이 있는 칼럼은 NaN으로 출력됩니다. - df.median()
- 중앙값(50분위수), 데이터를 오름차순 정렬하여 중앙에 위치한 값
- 이상치가 존채하는 경우, mean 보다 median을 대표값으로 선호
- 짝수개의 데이터가 있는 경우에는 가운데 2개 중앙 데이터의평균 값을 출력한다. - df.sum()
- 문자열 칼럼은 모든 데이터가 붙어서 출력될 수 있다. - df.var()
- 데이터의 값들이 평균으로 부터 얼마나 많이 흩뿌려져있는지를 나타낸다 - df.std()
- 표준편차 - df.agg([통계함수1, ...])
- 복수의 통계 함수 적용할때 사용하는 함수 - df.quantile()
- 주어진 데이터를 동등한 확률구간으로 분할하는 지점, 10%의 경우 0.1을, 80%의 경우 0.8대입하여 값을 구한다 - df.['column_name'].unique()
- 칼럼 내 고유값 - df.mode
- 가장많이 출현한 데이터 - df.corr()
- 상관관계
- 통계적 추정
- 모집단의 모수를 표본들의 통계값을 이용해서 추정하는 방법이다.
- 점추정(Point estimation)
- 모집단의 특성을 단일한 값으로 추정한다. - 편향(Bias)
- 추정량의 기댓값과 모수의 차이 - 평균제곱오차
- 오차의 제곱을 평균으로 나눈것, 0에 가까울 수록 추측한 값이 원본에 가깝기에 정확도가 높다고 볼 수 있다.
- 최대우도 추정량
- 우도함수(Likelihood function)
- 확률 변수의 결합확률밀도함수를 모수 θ에 대한 함수로 볼 때, 이를 우도함수 L이라고 한다.
=> 결합확률밀도함수가 모수에 대한 함수일때 우도함수라고 한다. - 확률 변수가 서로 독립이고 확률밀도함수 f(x; θ)에서 얻은 표본이라면

- 주어진 관찰값을 가장 잘 설명하는 모수 추정량이 된다.
- 우도함수(Likelihood function)
- 구간추정(Interval estimation)
- 모수가 있을 것으로 예상되는 구간을 정해놓고 해당 구간에 실제 모수가 있을 것으로 예상되는 확률은 구하는 것
- 점추정량은 추정된 값이 실제 모수와 얼마나 가까운지 알 수 없다.
- 신뢰도 : 설정한 구간에 실제로 모수 θ가 있을 확률
- 확률 구간 [a,b]에 대해 P(a < θ < b) = 1-α일때 1-α를 신뢰도, (1-α)*100% 를 신뢰구간
- 카이제곱 분포
- 주로 독립적인 표준 정규 분포를 따르는 확률변수들의 제곱합에 대한 분포를 나타낸다.
- 비대칭성 : 오른쪽으로 긴 꼬리를 가진 비대칭 분포, 왼쪽으로는 0에 근접, 오른쪽으론 무한대까지 연장가능
- 자유도(df) : 형태결정, 카이제곱 분포를 구성하는 독립적인 정규 분포의 수를 의미
- 적용 : 두 범주형 변수 사이의 독립성을 검정하는 카이제곱 검정, 모분산의 추정 및 검정, 적합도 검정,
다중 회귀 분석에서의 변수 선택 등 다양한 통계적 시험에서 사용된다. - 확률 밀도 함수 (자유도 k)

- 기대값과 분산 : 카이제곱 분포의 기대값은 자유도아 같고, 분산은 자유도의 두 배이다.
E(X) = k
Var(x) = 2k - 중심극한정리 : 자유도가 증가함에 따라 카이제곱 분포는 점점 정규 분포에 근사하게 된다.
- 누적 분포 함수 : 카이제곱 분포의 누적분포함수(CDF)는 일반적으로 수치적 방법을 통해 계산된다.

- 주로 독립적인 표준 정규 분포를 따르는 확률변수들의 제곱합에 대한 분포를 나타낸다.
- t-분포
- 작은 표본 크기의 데이터에서 모평균을 추정할 때 사용되는 확률 분포이다. 정규 분포와 유사하게 종 모양을 하고 있지만 꼬리가 더 무겁고 분포가 더 넓은 특성을 가진다.
- 자유도 k 인 확률 밀도 함수

- 모분산이 알려져 있지 않고 표본 크기가 작을 때 평균의 신뢰 구간을 추정하거나 가설 검정에 사용된다.
- 자유도가 증가함에 따라 t-분포는 정규 분포에 접근한다. (일반적으로 자유도 30이상 시 정규분포로 간주)
- f-분포
- 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산 비율을 나타낼때 사용가능
- 2개 이상의 표본 평균들이 동일한 모평균을 가진 집단에서 추출되었는지 or 서로 다른 모집단에서 추출된 것인지 판단할 때 사용
- 서로 독립인 두 확률변수 U와 V가 각각 자유도가 v1, v2인 카이제곱 분포를 따를 때, 새로운 확률 변수
F = (U/v1)/(V/v2) 는 자유도가 (v1,v2)인 F-분포를 따른다
- 모평균 구간추정
- 모분산 σ^2이 알려진 경우 모평균 μ의 100(1-α)% 신뢰구간은
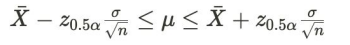
이때 Z0.5 α는 P(Z>z0.5 α) = 0.5 α를 만족하는 z값 - 가장 많이 사용하는 95% 신뢰구간의 경우 0.5 α = 0.025, z0.5 α = 1.96이다.
- 모분산을 모르는 경우(표본분산을 이용하는) 모평균 μ의 신뢰구간은

- 표본수가 30개 이상인데 모분산을 모르는 경우에도, 표본 수가 충분히 많으면 모집단이 정규분포라는 조건 없이도 표본분산은 모분산에 매우 가까워지므로 z-분포를 이용해 신뢰구간을 구할 수 있다.
- 모분산 σ2의 100(1-α)% 신뢰구간은

- 모분산 σ^2이 알려진 경우 모평균 μ의 100(1-α)% 신뢰구간은
- 모비율 구간추정
- 표본비율 : 이항분포를 따르는 모비율이 p인 사건이 n개의 표본 중 X개가 나타났을 때

- 표본비율의 기댓값 = p, 분산 = p(1-p)n
- 모비율이 p인 이항분포에서 충분히 많은 n개의 표본으로부터 나온 표본비율에 대해 모비율p의 100(1-α)% 신뢰
구간은
- 표본비율 : 이항분포를 따르는 모비율이 p인 사건이 n개의 표본 중 X개가 나타났을 때
- 가설검정
- 통계적 가설검정 : 표본에서 얻은 사실을 근거로 하여 모집단에 대한 가설이 맞는지 통계적으로 검정하는 방법
- 귀무가설(Null hypothesis, H0) : 직접 검정대상이 되는 가설
- 먼저 증명된 적 없는 이 귀무가설이 일단 옳다는 가정 하에 검정을 시작하며, 보통은 귀무가설이 진실일
가능성이 적기에 기각을 목표로 가설을 새운다 - 대립가설(Alternative hypothesis, H1) : 귀무가설의 반대가 되는 가설
- 보통은 새로운 주장 혹은 실제로 입증시키고 싶은 가설이며 귀무가설이 기각되면 자동적으로 채택되도록 설계 - 유의수준(Level of significance, α) : 귀무가설이 실제로 옳음에도 기각하는 오류
- 귀무가설이 실제로는 맞지만 틀리다고 할 수 있는 확률, 위험부담 보통 0.05로 값을 설정 - 임계값(Critical value) : 유의수준이 주어졌을때 귀무가설의 채택과 기각 의사를 결정하는 기준이 되는 값
- 가설검정의 오류
- 제 1종 오류 (type 1 error) : 귀무가설이 참임에도 이를 기각하는 오류
- 제 2종 오류 (type 2 error) : 귀무가설이 거짓임에도 이를 채택하는 오류
- α(유의수준) = P(type 1 error) = P(H0를 기각 | H0는 참)
β = P(type 2 error) = P(H0를 채택 | H0는 거짓) - α와 β의 크기는 서로 상반되기 때문에 동시에 줄일 수없다, 표본의 크기를 증가시키면 분산이 작아지기 때문에
오류의 확률이 줄어든다.
- 단측검정과 양측검정
- 단측검정(One-sided test) : 대립가설 H1이 어떤 특정값 이상 / 이하 라고 설정되는 경우의 검정
- 양측검정(Two-sided test) : H0: μ=μ0, H1: μ!=μ0
- 유의 수준을 반으로 나누고 기각역을 양쪽에 설정한다.
- 모평균 가설검정
- 모평균의 구간 추정과 같이 모분산을 아는 경우와 모르는 경우로 나눠서 접근한다.
- 모분산을 아는 경우 검정통계량


- 모분산을 모르는 경우에는 t-분포를 이용해서 기각역을 구해야됩니다.
검정통계량 T는 표본분산을 이용해서

- 모평균 차에 대한 가설검정
- 두 개의 모집단에 대한 가설검정 진행가능하다
- 두 집단의 모분산을 아는 경우

- 두 집단의 모분산을 모르는 경우

- 위의 두 식을 이용하여 검정통계량을 계산 후 각각 표준정규분포, t-분포를 이용한 기각역과 비교하여 검정
- 모분산 비에 대한 가설 검정
- 귀무가설 H0: 두 모집단의 분산이 같다 ((σ1)^2=(σ2)^2)
- 검정통계량 : F = (S1)^2 / (S2)^2
- 양측검정 : F ≧ F0.5α(n1-1, n2-1), F ≦ F1-0.5α(n1-1,n2-1)
- 우측 단층검정 : F ≧ Fα(n1-1, n2-1)
좌측 단층검정 : F ≦ F1-α(n1-1,n2-1)
- ANOVA(analysis of variance, 분산분석)
- n개의 집단을 비교하는통계적 분석(n > 2)
- n > 2 인 경우 n개의 집단에서 t-검정을 하는 경우 문제 발생
- 분산분석은 사용하기전 3가지 조건을 만족해야한다.
- 정규성 : 모든 데이터가 정규분포를 따르는 모집단으로부터 추출된다.
- 정규분포를 따르지 않는 것으로 보이는 경우 Log 변환 등의 전처리가 필요할 수 있습니다 - 독립성 : 모든 데이터가 모집단으로부터 독립적으로 추출된다.
- 등분산성 : 모든 데이터는 분산이 동일한 모집단들로 부터 추출된다.
- 보통은 가장 큰 분산과 작은 분산의 비가 4:1정도를 넘지 않으면 ANOVA를 적용해도 괜찮은 것으로 본다.
- 정규성 : 모든 데이터가 정규분포를 따르는 모집단으로부터 추출된다.
- 임원 분산분석(one-way ANOVA)
- 집단의 종류(분산분석)가 하나이고 집단들이 가지는 평균값(종속 변수)이 하나인 경우 그 집단간 모평균의 차이
여부를 검증하는 방법 - 귀무가설 H0: μgroup1=...=μgroup m=μ (m= 그룹 수)
대립가설 H1: 적어도 한 쌍의 모평균은 같지 않음
- MSB(Mean squares between, 그룹간 분산) = SSB / dfB = SSB / (m-1)
- MSE(Mean squares error, 그룹내 분산) = SSE / dfE = SSE / m(n-1)
- 분산비 F = MSB / MSE
(df : degree of freedom, 자유도) - 여기서 구한 분산비 F는 자유도가 (k-1, n-k)인 F분포를 따릅니다.
- H0는 ‘각 집단간 평균이 같다’ 이므로 맞다면 MSB가 MSE보다 작아야 된다.
=> 이 F값과 유의수준 α, 자유도 (k-1, n-k)를 이용해서 우측 단측검정(F=MSB/MSE>1)을 진행

공부하며 어려웠던 점
- 기초 통계를 단시간에 배웠는데 어려웠다
반응형
'데이터분석' 카테고리의 다른 글
| 33-(2). Matplotlib (1) | 2024.01.15 |
|---|---|
| 33-(1) Matplotlib Visualization - 기본문법 (1) | 2024.01.14 |
| 32-(1). 확률과 통계 (2) | 2024.01.14 |
| 31. 정규화, 데이터 스케일링 (2) | 2024.01.10 |
| 30. 문자열 제어 및 DataFrame 재구성 (0) | 2024.01.09 |